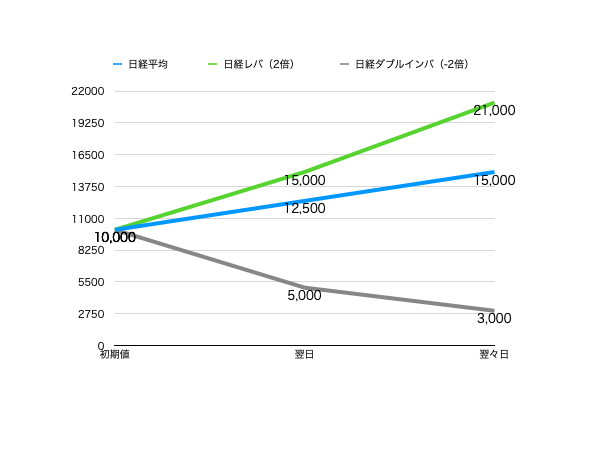
【緊急解説】注意!! レバレッジ(ブル2倍)型ETF/ダブルインバース(ベア2倍)型ETFの盲点
〜 2倍儲かってるはずが…… あれ? 〜
レバレッジ(±2倍)型ETFが人気だ
レバレッジ(±2倍)型ETFとはどんな商品なのでしょうか?
東京証券取引所HPにあるパンフレットから読み解くと
日経平均レバレッジ型ETF
指数の変動率が、日経平均株価の前日比変動率(%)の2倍となるように計算された、日経平均レバレッジ・インデックスに連動を目指すETF(上場投資信託)です。
つまり、日経平均が上昇したらその2倍儲かり、下落したらその2倍損するということ……
日経平均ダブルインバース型ETF
指数の変動率が、日経平均株価の前日比変動率(%)の-2倍となるように計算された、日経平均ダブルインバース・インデックスに連動するETF(上場投資信託)です。
つまり、日経平均が下落したらその2倍儲かり、上昇したらその2倍損するということ……
それでは実際の値動きを見てみましょう
1.長期の値動き
日経平均レバレッジ・インデックスの値動き
日経平均レバレッジ・インデックスの算出開始は2011年6月6日。2001年12月28日の値を10,000とし、現在は東京証券取引所が開場している時間帯に5秒間隔で算出しています
| 2001年12月28日終値 | 2020年4月24日終値 | 騰落率 | |
| 日経平均 | 13785.69 | 19262.00 | 39.7% |
| 日経平均レバレッジ・インデックス | 10000 | 12366.34 | 23.7% |
日経平均の騰落率の2倍どころか1倍もいってないですね!
日経平均ダブルインバース・インデックスの値動き
日経平均ダブルインバース・インデックスの公表開始は2014年6月16日。2001年12月28日の値を100,000とし、現在は東京証券取引所が開場している時間帯に5秒間隔で算出しています
| 2001年12月28日終値 | 2020年4月24日終値 | 騰落率 | |
| 日経平均 | 13785.69 | 19262.00 | 39.7% |
| 日経平均ダブルインバース・インデックス | 10000 | 1574.95 | -84.3% |
日経平均の騰落率の-2倍以上に下落していますね!
実は中長期では、日経平均株価の騰落率の2倍と必ずしも連動しないんです
理由はいくつかありますが、特に重要と思われるのは
日経平均株価の前日比変動率(%)の2倍(-2倍)となるように計算された
という部分です
どういうことか、次の項で説明します
2.変動パターン
日経平均株価の動きと日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスの価格変化を変動パターン別に見ていきたいと思います
わかりやすくするために、スタートを以下のように設定します
日経平均株価:10,000円
日経平均レバレッジ・インデックス:10,000円
日経平均ダブルインバース・インデックス:10,000円
変動パターンは以下の通り
①日経平均が翌日25%上昇
②日経平均が翌日20%下落
③日経平均が翌日25%上昇、翌々日20%下落
④日経平均が翌日20%下落、翌々日25%上昇
⑤日経平均が翌日25%上昇、翌々日20%上昇
⑥日経平均が翌日25%下落、翌々日20%下落
※注意:
日経平均株価は東証225銘柄で構成されており、それぞれの株価の価格帯別にストップ高・ストップ安が設定されています
よって、実際に1日で日経平均株価が20%以上の上昇・下落を示すことはかなり極端なケースと考えられます
ここでは、わかりやすくするために極端な数値を用いていることをご了承ください
①日経平均が翌日25%上昇
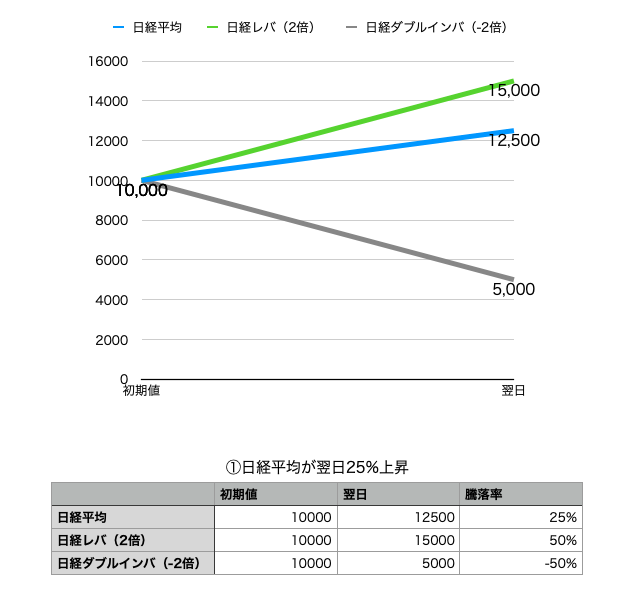
日経平均株価の騰落率に対して、日経平均レバレッジ・インデックスは2倍の騰落率、日経平均ダブルインバース・インデックスは−2倍の騰落率でこれは納得ですよね
②日経平均が翌日20%下落
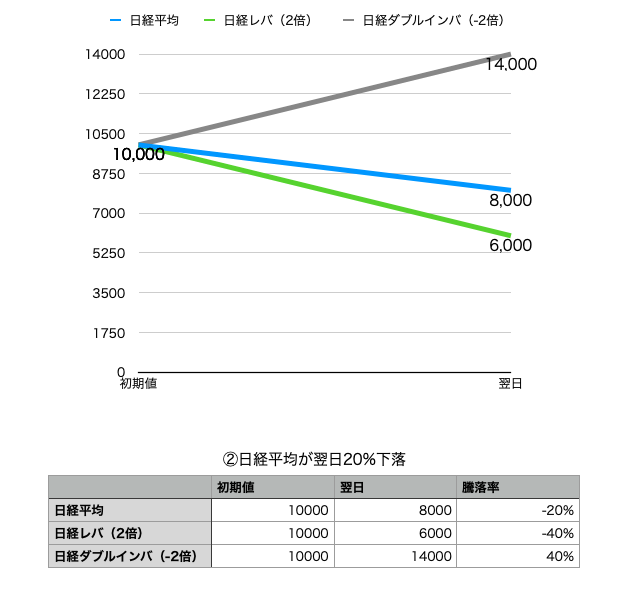
日経平均株価の騰落率に対して、日経平均レバレッジ・インデックスは2倍の騰落率、日経平均ダブルインバース・インデックスは−2倍の騰落率でこれも納得ですよね
③日経平均が翌日25%上昇、翌々日20%下落
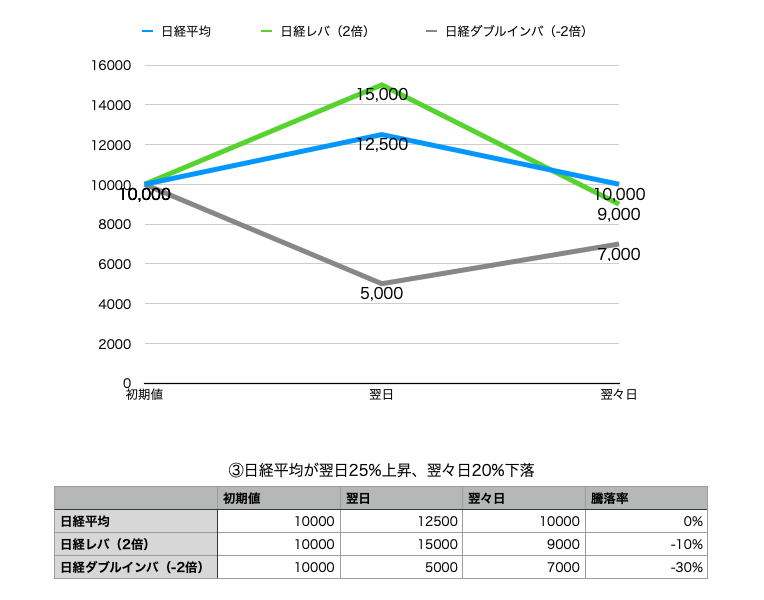
日経平均株価はプラスマイナスゼロで変わらずなのに 、日経平均レバレッジ・インデックスは−10%、日経平均ダブルインバース・インデックスは−30%ってひどいですよね
④日経平均が翌日20%下落、翌々日25%上昇
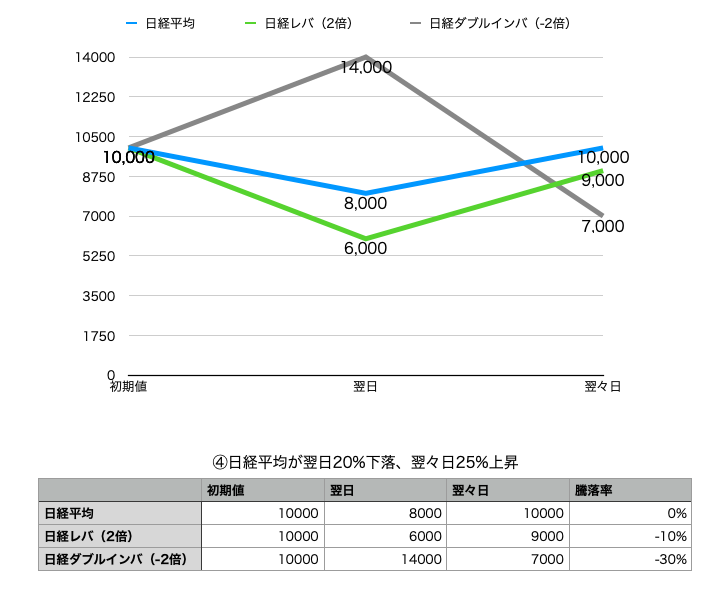
これも同じですよね、日経平均株価はプラスマイナスゼロで変わらずなのに 、日経平均レバレッジ・インデックスは−10%、日経平均ダブルインバース・インデックスは−30%ってひどいですよね
値上がりと値下がりが入れ替わっても損益は変わらないですね
⑤日経平均が翌日25%上昇、翌々日20%上昇
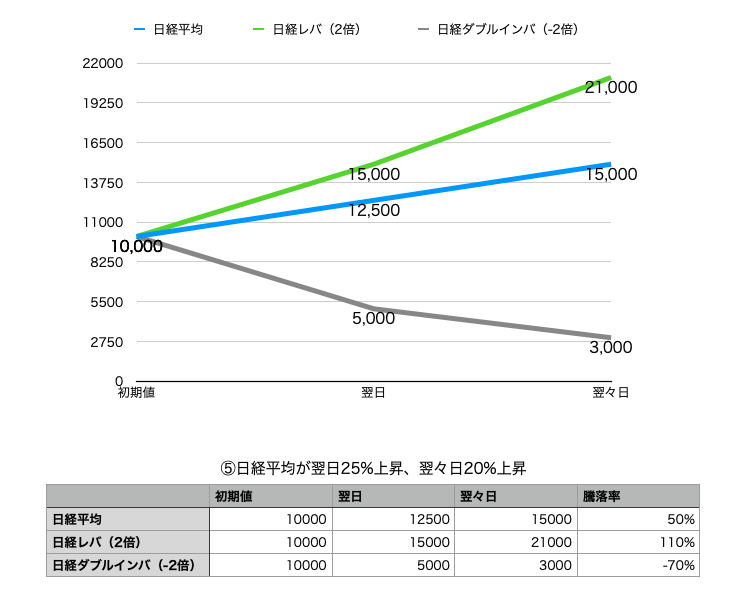
連続上昇のケースです
日経平均株価の上昇率50%に対して、
日経平均レバレッジ・インデックスはその2倍100%より10%多い110%の上昇率になっています
また、日経平均ダブルインバース・インデックスは−2倍であれば50%×−2=−100%でゼロになるところが、−70%で済んでいます
⑥日経平均が翌日25%下落、翌々日20%下落
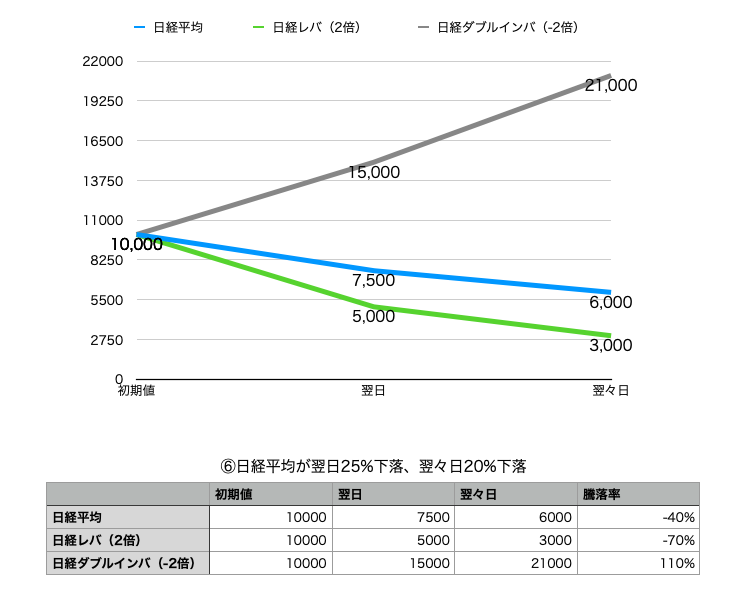
連続下落のケースです
日経平均株価の下落率40%に対して、
日経平均レバレッジ・インデックスはその2倍ー80%より10%少ない70%の下落で済んでいます
また、日経平均ダブルインバース・インデックスは−2倍であれば−40%×−2=80%のところが、30%も多い110%のプラスになっています
推論
上記6つのパターン分析から以下のようなことが推察されます
- 日経平均株価の翌日の騰落率と翌々日の騰落率が入れ替わっても、日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスの騰落率は変化しない
- 日経平均株価の翌日の騰落率と翌々日の騰落率のプラスマイナスが入れ替わる場合(上昇下降もしくは下降上昇)、日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスの騰落率は日経平均株価の騰落率の2倍/−2倍より劣る
- 日経平均株価の翌日と翌々日が連続して上昇または下落する場合、日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスの騰落率は日経平均株価の騰落率の2倍/−2倍より有利に働く
3.数学的に表してみる
原資産である日経平均株価の翌日の騰落率をα、翌々日の騰落率をβとして、翌々日の日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスの騰落率を考えてみる
日経平均株価のリターン:Rnk
日経平均レバレッジ・インデックスのリターン:Rle
日経平均ダブルインバース・インデックスのリターン:Rwi
とします
翌日の日経平均株価のリターン
Rnk=α
翌日の日経平均レバレッジ・インデックスのリターン
Rle=2α
翌日の日経平均ダブルインバース・インデックスのリターン
Rwi=-2α
翌々日の日経平均株価のリターン
Rnk=(1+α)(1+β)-1
=α+β+αβ
日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスのリターンとの関係を表すために以下の式を用意します
両辺を2倍する
2Rnk=2α+2β+2αβ
2α+2β=2Rnk-2αβ………………①
翌々日の日経平均レバレッジ・インデックスのリターン
Rle=(1+2α)(1+2β)-1
=2α+2β+4αβ
①を代入
Rle=(2Rnk-2αβ)+4αβ
=2Rnk+2αβ
つまり、翌々日の日経平均レバレッジ・インデックスのリターンは日経平均株価のリターンの2倍と、日経平均株価の翌日の騰落率α、翌々日の騰落率βを掛け合わせて2倍した分ズレが生じることとなる
数式より翌々日の日経平均レバレッジ・インデックスのリターンは
連続上昇(α>0,β>0)の場合
2αβ>0となり
日経平均株価の上昇率の2倍より2αβ分上昇率は大きくなる
連続下落(α<0,β<0)の場合
2αβ>0となり
日経平均株価の下落率の2倍より2αβ分下落率は小さくなる
上昇・下落(α>0,β<0)または下落・上昇(α<0,β>0)の場合
2αβ<0となり
日経平均株価のリターンの2倍より2αβ分リターンは減少する
翌々日の日経平均ダブルインバース・インデックスのリターン
Rwi=(1-2α)(1-2β)-1
=-2α-2β+4αβ
=-(2α+2β)+4αβ
①を代入
Rle=-(2Rnk-2αβ)+4αβ
=-2Rnk+6αβ
つまり、翌々日の日経平均レバレッジ・インデックスのリターンは日経平均株価のリターンの2倍と、日経平均株価の翌日の騰落率α、翌々日の騰落率βを掛け合わせて6倍した分ズレが生じることとなる
数式より翌々日の日経平均レバレッジ・インデックスのリターンは
連続上昇(α>0,β>0)の場合
6αβ>0となり
日経平均株価の上昇率の-2倍より6αβ分下落率は小さくなる
連続下落(α<0,β<0)の場合
2αβ>0となり
日経平均株価の下落率の-2倍より6αβ分上昇率は大きくなる
上昇・下落(α>0,β<0)または下落・上昇(α<0,β>0)の場合
6αβ<0となり
日経平均株価のリターンの2倍より6αβ分リターンは減少する
現実的な考察
前々項ではわかりやすく表現するために、日経平均株価が20%以上の上昇・下落するケースを考察しましたが、現実的な値動きを想定し
①日経平均が翌日1%下落、翌々日1%上昇
②日経平均が翌日1%上昇、翌々日1%上昇
③日経平均が翌日1%下落、翌々日1%下落
のケースで日経平均株価と日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスの変化を考えてみましょう
①日経平均が翌日1%下落、翌々日1%上昇
日経平均株価
Rnk=(1+α)(1+β)-1
=α+β+αβ
=-0.01+0.01-0.0001
=-0.0001 [-0.01%]
日経平均株価が10,000円であれば−1円の変化
日経平均レバレッジ・インデックス
Rle=(2Rnk-2αβ)+4αβ
=2Rnk+2αβ
=2(-0.0001)+2(-0.01)(0.01)
=-0.0004[-0.04%]
日経平均株価の騰落率×2倍との差分
2αβ=2(-0.01)(0.01)=-0.0002 [-0.02%]
日経平均ダブルインバース・インデックス
Rle=-(2Rnk-2αβ)+4αβ
=-2Rnk+6αβ
=-2(-0.0001)+6(-0.01)(0.01)
=-0.0004[-0.04%]
日経平均株価の騰落率×2倍との差分
6αβ=6(-0.01)(0.01)=-0.0006 [-0.06%]
②日経平均が翌日1%上昇、翌々日1%上昇
日経平均株価
Rnk=(1+α)(1+β)-1
=α+β+αβ
=0.01+0.01+0.0001
=0.0201 [2.01%]
日経平均株価が10,000円であれば201円の変化
日経平均レバレッジ・インデックス
Rle=(2Rnk-2αβ)+4αβ
=2Rnk+2αβ
=2(0.0201)+2(0.01)(0.01)
=0.0404[4.04%]
日経平均株価の騰落率×2倍との差分
2αβ=2(0.01)(0.01)=0.0002 [0.02%]
日経平均ダブルインバース・インデックス
Rle=-(2Rnk-2αβ)+4αβ
=-2Rnk+6αβ
=-2(0.0201)+6(0.01)(0.01)
=-0.0396[-3.96%]
日経平均株価の騰落率×2倍との差分
6αβ=6(0.01)(0.01)=0.0006 [0.06%]
③日経平均が翌日1%下落、翌々日1%下落
日経平均株価
Rnk=(1+α)(1+β)-1
=α+β+αβ
=-0.01-0.01+0.0001
=-0.0199 [-1.99%]
日経平均株価が10,000円であれば−199円の変化
日経平均レバレッジ・インデックス
Rle=(2Rnk-2αβ)+4αβ
=2Rnk+2αβ
=2(-0.0199)+2(-0.01)(-0.01)
=-0.0396[-3.96%]
日経平均株価の騰落率×2倍との差分
2αβ=2(0.01)(0.01)=0.0002 [0.02%]
日経平均ダブルインバース・インデックス
Rle=-(2Rnk-2αβ)+4αβ
=-2Rnk+6αβ
=-2(-0.0199)+6(0.01)(0.01)
=-0.0404[-4.04%]
日経平均株価の騰落率×2倍との差分
6αβ=6(0.01)(0.01)=0.0006 [0.06%]
結論
日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスともに上昇・下落を繰り返す相場では日経平均株価の2倍のパフォーマンスを得られない可能性がある
その可能性は日経平均レバレッジ・インデックスと比較して日経平均ダブルインバース・インデックスで顕著である
また、逆に連続上昇、連続下落の多い局面では、日経平均レバレッジ・インデックス/日経平均ダブルインバース・インデックスそれぞれ日経平均株価の2倍のパフォーマンス以上のリターンを得られる可能性がある
4.参考資料
他、参考資料
レバレッジ型ETFの落とし穴(ニッセイ基礎研究所 金融研究部 チーフ株式ストラテジスト・年金総合リサーチセンター兼任 井出 真吾)